Create a backtransform morphospace
This tutorial will show you how to create a "backtransform morphospace" (both non-phylogenetic and phylogenetic) in R (below). A backtransform morphospace takes a standard morphospace plot, which groups objects or biological specimens according to how similar they are in shape, and adds representative shapes in a grid pattern across the plot to show intuitively how shape varies across morphospace (Olsen 2017).
These shapes placed into the background of the plot are "backtransformations" from a principal coordinates analysis, which identifies the major axes of variation with a shape dataset. Importantly, these backtranform shapes are not actual shapes within the input dataset. Rather they are theoretical shapes that represent a combination of two particular PC (principal component) scores and the mean of all the other PC scores. An alternative way to think of these backtransform shapes is that they are the shape an object or specimen would have if it were at a particular point in a 2D morphospace (e.g. at a particular value of PC1 and PC2) and at the average position along all other PC axes.
If most of your shape variation can be condensed into a few PC scores then these theoretical shapes will correspond well to the shapes in the input dataset. A useful feature of a backtransform morphospace is that it shows what shapes look like throughout the entire morphospace, rather than just where you have samples, to create an even distribution for visualization.
If you are using this code for a publication please cite the following paper:
Preliminary steps
All of the code in this tutorial are R commands. So be sure you have R installed on your system. If you do not have R installed you can find installation instructions here.
You will also need to have the R packages geomorph and StereoMorph installed. The geomorph package will allow you to perform the Generalized Procrustes Analysis and the StereoMorph package has the function for creating the backtransform morphospace. For StereoMorph be sure that you have a version equal to or greater than 1.6.2 installed since this has the btShapes function. If you have not installed these packages you can install them using the install.packages function.
# Install R packages (if not installed already) install.packages('geomorph', dependencies=TRUE) install.packages('StereoMorph', dependencies=TRUE)
Once the package is installed, load it into the current R environment using the library function.
# Load the packages library(geomorph) library(StereoMorph)
Creating a (non-phylogenetic) backtransform morphospace using 3D shape data
The main part of this tutorial will first demonstrate making a backtransform morphospace using 3D shape data and a non-phylogenetic principal components analysis (PCA). Creating a phylogenetic morphospace or using 2D shape data requires only a few modifications to this code, which are detailed after this section.
First we need shape data to plot. These should be landmarks or curve points (either two- or three-dimensional) saved in a three-dimensional array in which the first array dimension is the point names, the second dimension is the xy-coordinates (or xyz-coordinates for 3D data), and the third dimension is each individual/species/etc. For this tutorial we'll use 3D landmark and curve points collected from waterfowl bird beaks, originally published in this paper looking at the correlation between beak shape and diet in waterfowl. You can download these data from datadryad by clicking here. Unzip this folder and move it to your current working directory.
Read the example shape data from the 'Beak shape by species' folder.
# Read all files in "Beak shape by species" folder into list read_files <- lapply(paste0('Beak shape by species/', list.files('Beak shape by species')), 'read.table')
Convert the shape data from list of matrices into a three-dimensional array, specifying names along the first and third dimension of the array. This should create a 150 x 3 x 51 dimension array.
# Convert list of shape data into array lm_array <- array(unlist(read_files), dim=c(dim(read_files[[1]]), length(read_files)), dimnames=list(rownames(read_files[[1]]), NULL, gsub('[.]txt$', '', list.files('Beak shape by species'))))
Perform Generalized Procrustes Analysis (GPA) using the geomorph function gpagen to obtain Procrustes coordinates. GPA scales each shape to the same centroid size and optimally aligns the shapes (using translation and rotation) based on homologous points to remove differences due simply to differences in position and orientation.
# Get generalized Procrustes coordinates gpa_array <- gpagen(lm_array)$coords
Perform a (non-phylogenetic) principal components analysis (PCA) to identify the major axes of shape variation.
# Convert array to matrix for PCA gpa_mat <- t(apply(gpa_array, 3, function(y) matrix(t(y), 1))) # Perform non-phylogenetic PCA resEig <- eigen(cov(gpa_mat)) # Get PC scores scores <- gpa_mat %*% resEig$vectors # Get percent variance explained along each axis per_var <- (resEig$values / sum(resEig$values))*100
In order to plot each backtransform shape we need to create a function that will take our shape coordinates and produce a graphic of the specimen or object. For example, the function could connect a series of neighboring landmarks to create an outline. How you draw the shape data depends on what kind of shape data you have and how you want the graphic to look, so you will have to create this function yourself. But the function included in this example should serve as a useful template.
You can name the function whatever you'd like. The example below is named plot_beak_lateral. This function takes curve points along the bottom and top margin of the beak and creates a silhouette of the beak from a lateral view. The shape data that are input to this function are 3D so this function just takes a simple projection of the 3D shape onto the midline body plane. You could rotate the entire shape before taking the projection to get a top-down view instead of a lateral view.
The first two parameters to this function have to be the following:
- xy: a 2-column matrix of the PC scores where each backtransform shape will be drawn
- coor: a matrix of the shape coordinates for each backtransform shape (2-column for 2D and 3-column for 3D)
You can include any number of extra parameters that you would like to customize the shape drawing. In the example below there is a size parameter to adjust the overall size of each backtransform shape and a color parameter to specify the fill color of the beaks. The extra parameters that you specify will be passed along through the btShapes function (the function you create will be called by btShapes) so they should differ from the input parameters to btShapes.
# Define function to draw shape plot_beak_lateral <- function(xy, coor, size=1, col='black'){ # If 3D, rotate points about x-axis using 3D rotation matrix if(ncol(coor) == 3){ coor <- coor %*% matrix(c(1,0,0, 0,cos(-pi/2),sin(-pi/2), 0,-sin(-pi/2),cos(-pi/2)), nrow=3, ncol=3) } # Get just x,y coordinates (orthographic projection into xy-plane) coor <- coor[, 1:2] # Get plot aspect ratio w <- par('pin')[1]/diff(par('usr')[1:2]) h <- par('pin')[2]/diff(par('usr')[3:4]) asp <- w/h # Correct for plot aspect ratio not necessarily being 1:1 coor[, 1] <- coor[, 1] * (1/asp) # Scale points and place back in position coor <- coor*size # Center about zero based on range of coordinates coor <- coor - matrix(colMeans(apply(coor, 2, range)), nrow=nrow(coor), ncol=ncol(coor), byrow=TRUE) # Move shape to PC score coor <- coor + matrix(xy, nrow(coor), ncol(coor), byrow=TRUE) # Set order in which to draw points to create polygon polygon_order <- c(which(grepl('upper_bill_culmen', rownames(coor))), rev(which(grepl('upper_bill_tomium_L', rownames(coor))))) # Create filled polygon polygon(coor[polygon_order, ], col=col, border=col) }
To use this function in other projects you might want to save this function to its own file, for example 'plot_beak_lateral.R' and then load the function at the start of your code using the source function.
Set the two PC axes that you want to plot. For this example we'll plot the first and second PC axes. These are the two PC axes that form the basis of the grid onto which the backtransform shapes are drawn (the shapes will use the average PC scores along all the remaining axes).
# Set PCs to plot pcs <- 1:2
For this tutorial we'll create a plot as a PDF file. Open a PDF graphics device where the plot will be produced.
# Open PDF graphics device pdf('Backtransform PCA.pdf', width=9, height=6.5)
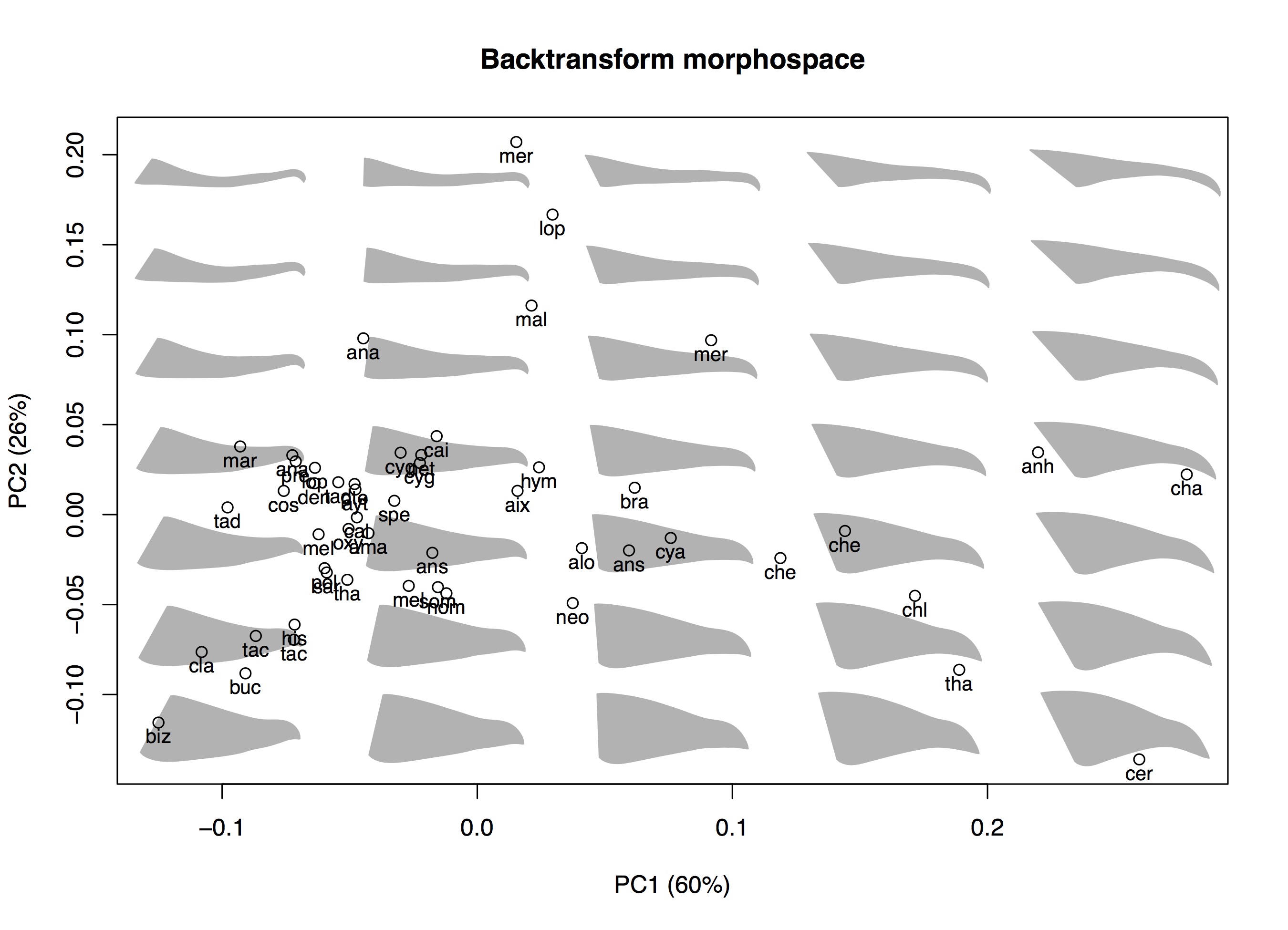
Create a plot box with axes and axis labels. Use the n value for the type parameter to draw the plot without plotting the scores. That way you can add the scores later on top of the backtransform shapes.
# Create plot box with axes and axis labels plot(scores[, pcs], type='n', main='Backtransform morphospace', xlab=paste0('PC', pcs[1], ' (', round(per_var[pcs[1]]), '%)'), ylab=paste0('PC', pcs[2], ' (', round(per_var[pcs[2]]), '%)'))
Plot the backtransform shapes in the plot box using the btShapes function.
# Plot backtransform shapes btShapes(scores=scores, vectors=resEig$vectors, fcn=plot_beak_lateral, pcs=pcs, n=c(5,7), m=dim(lm_array)[2], row.names=dimnames(lm_array)[[1]], pc.margin=c(0.06,0.05), size=0.5, col=gray(0.7))
Here are the input parameters to btShapes:
- scores: a matrix of the PCA scores
- vectors: a matrix of the PCA eigenvectors
- fcn: the function that will be called by btShapes to draw each shape
- pcs: the two PC axes for the plot
- n: a two-element vector giving the number of shapes to draw along the x- and y-axes, respectively
- m: number of shape dimensions (2 for 2D, 3 for 3D)
- row.names: a vector giving the names of the landmarks in the same order as the shape array input to the PC analysis
- pc.margin: a two-element vector giving the margins along the x- and y-axes, respectively, for the range of PC scores that are used to draw the shapes. For example, a value of 0.05 will start drawing the backtransform shapes at values 5% greater than the minimum PC score along the corresponding axis and end at 5% less than the maximum PC score. This is useful for making sure the shapes fall within the plot box.
The remaining two input parameters (size and col) are inputs to the plot_beak_lateral function so these may differ depending on how you write your shape drawing function.
If you'd like, you can then plot the points for each species on top of the backtransform shapes.
# Plot points for each species points(scores[, pcs])
Add text labels.
# Add text labels text(scores[, pcs], labels=substr(rownames(scores), 0, 3), cex=0.8, pos=1, offset=0.3)
Close the PDF graphics device.
# Close the PDF graphics device dev.off()
This should produce the following plot:
Creating a phylogenetic backtransform morphospace
The previous section showed how to use a non-phylogenetic PCA to find the major axes of shape variation. However, PCA assumes that each of the data points are independent samples from a population (like a standard linear regression). Since sampled taxa are not independent of one another but in fact related to each other you might want to incorporate the phylogeny for your taxa into the PCA analysis to account for this non-independence. Another way to think about this is that if you had a sample in which many taxa were all closely related and just a few distantly related taxa, you wouldn't want the many closely related specimens to have an outsized influence in determining the PC axes (see Revell 2009 for a nice explanation of this). This section will show you how to create a backtransform morphospace onto a phylogenetic PCA (pPCA) plot.
Before starting this section make sure you've worked through the previous section. There is some overlap in the code needed for the previous section and for this section so it's assumed that you have run all of the previous code in the current workspace. Before starting also make sure you have the following additional R packages installed.
# Install ape and phytools (if not already installed) install.packages('ape', dependencies=TRUE) install.packages('phytools', dependencies=TRUE)
Then load the packages into the current R environment.
# Load the packages library(ape) library(phytools)
Next, find a tree for your sampled taxa. You can download the tree for this tutorial by clicking here. Save this file in the web browser using 'File > Save' (be sure the file saves with a '.tre' extension and not '.txt'). Then move this tree file ('Burleigh, Kimball, Braun, 2015 ML Tree, pruned.tre') to your current R working directory. This tree comes from a larger tree by Burleigh, Kimball & Braun 2015 and has been pruned down to include just the species in this tutorial.
Load the tree using the read.tree function from the ape package.
# Read tree tree <- read.tree(file='Burleigh, Kimball, Braun, 2015 ML Tree, pruned.tre')
You can use the same gpa_mat from the generalized Procrustes coordinates that you created in the previous section but this time it will be used to perform a pPCA instead of a PCA, using the phyl.pca function from the phytools package.
# Perform phylogenetic PCA phyl_pca <- phyl.pca(tree, Y=gpa_mat, method='BM')
From the phyl.pca results you can get the pPCA scores, eigenvectors, and percent variance explained by each axis, just as for a non-phylogenetic PCA.
# Get PC scores ppca_scores <- phyl_pca$S # Get PC eigenvectors ppca_vectors <- phyl_pca$Evec # Get percent variance explained along each axis diag_values <- phyl_pca$Eval[diag(nrow(phyl_pca$Eval)) == TRUE] ppca_per_var <- (diag_values / sum(diag_values, na.rm=TRUE))*100
Lastly get a vector of the phylogenetic means using the covariance and variance-covariance matrices. This will be input into btShapes.
# Find covariance matrix due to phylogenetic relatedness cov_mat <- vcv.phylo(tree)[rownames(gpa_mat), rownames(gpa_mat)] # Compute the phylogenetic trait variance-covariance matrix to get the phylogenetic means phy_means <- phyl.vcv(gpa_mat, cov_mat, 1)$alpha
Set the two PC axes that you want to plot, just as in the previous section.
# Set PCs to plot pcs <- 1:2
Open a PDF graphics device where the plot will be produced and create a plot box with axes and axis labels. Use the n value for the type parameter to draw the plot without plotting the scores. That way you can add the scores later on top of the backtransform shapes.
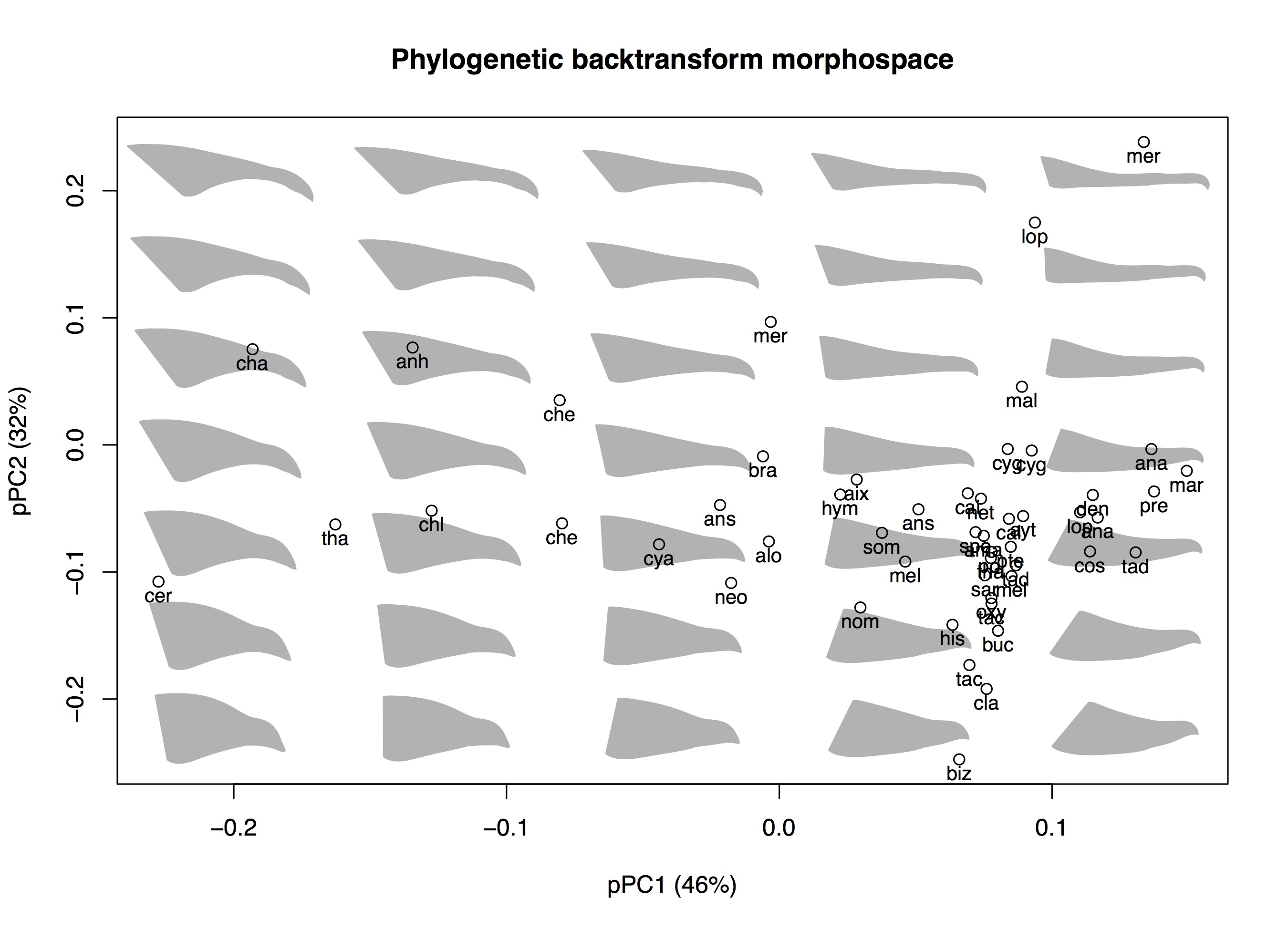
# Open PDF graphics device pdf('Backtransform pPCA.pdf', width=9, height=6.5) # Create plot box with axes and axis labels plot(ppca_scores[, pcs], type='n', main='Phylogenetic backtransform morphospace', xlab=paste0('pPC', pcs[1], ' (', round(ppca_per_var[pcs[1]]), '%)'), ylab=paste0('pPC', pcs[2], ' (', round(ppca_per_var[pcs[2]]), '%)'))
Plot the backtransform shapes into the current plot using the btShapes function. This function call uses the same input parameters as for the non-phylogenetic PCA with one additional parameter for the phylogenetic means, phy.means. Note that now you'll input the pPCA scores and vectors instead of the PCA scores and vectors.
# Plot backtransform shapes btShapes(scores=ppca_scores, vectors=ppca_vectors, fcn=plot_beak_lateral, pcs=pcs, n=c(6,8), m=dim(lm_array)[2], row.names=dimnames(lm_array)[[1]], pc.margin=c(0.06,0.05), phy.means=phy_means, size=0.5, col=gray(0.7))
Add the scores and labels onto the plot, if you'd like.
# Plot points for each species points(ppca_scores[, pcs]) # Add text labels text(ppca_scores[, pcs], labels=substr(rownames(ppca_scores), 0, 3), cex=0.8, pos=1, offset=0.3)
And close the connection to the PDF graphics device.
# Close the PDF graphics device dev.off()
This should produce the following plot:
It's interesting to now compare the two plots side by side. Looking at the relative positions of the points, adding the phylogeny the PCA hasn't substantially changed the positions of the points relative to one another. Rather it has taken all of the points and rotated them about 30-45 degrees relative to the center of the plot. This has the effect of changing the axes of shape variation that are orthogonal (uncorrelated) with one another.
For this particular dataset there is an interesting phylogenetic pattern in that a more goose-like beak (more toward the left in the pPCA morphospace) has evolved convergently multiple times in waterfowl, probably at least six times (Olsen 2017). Once phylogeny is taken into account the variation between a more duck-like beak (probably ancestral) and a more goose-like beak weighs more heavily on the PCA (because they represent more 'independent' transitions). The end effect is that the axis differentiating duck and goose beaks is more squarely aligned with the first PC axis in the pPCA (right) than in the PCA (left).
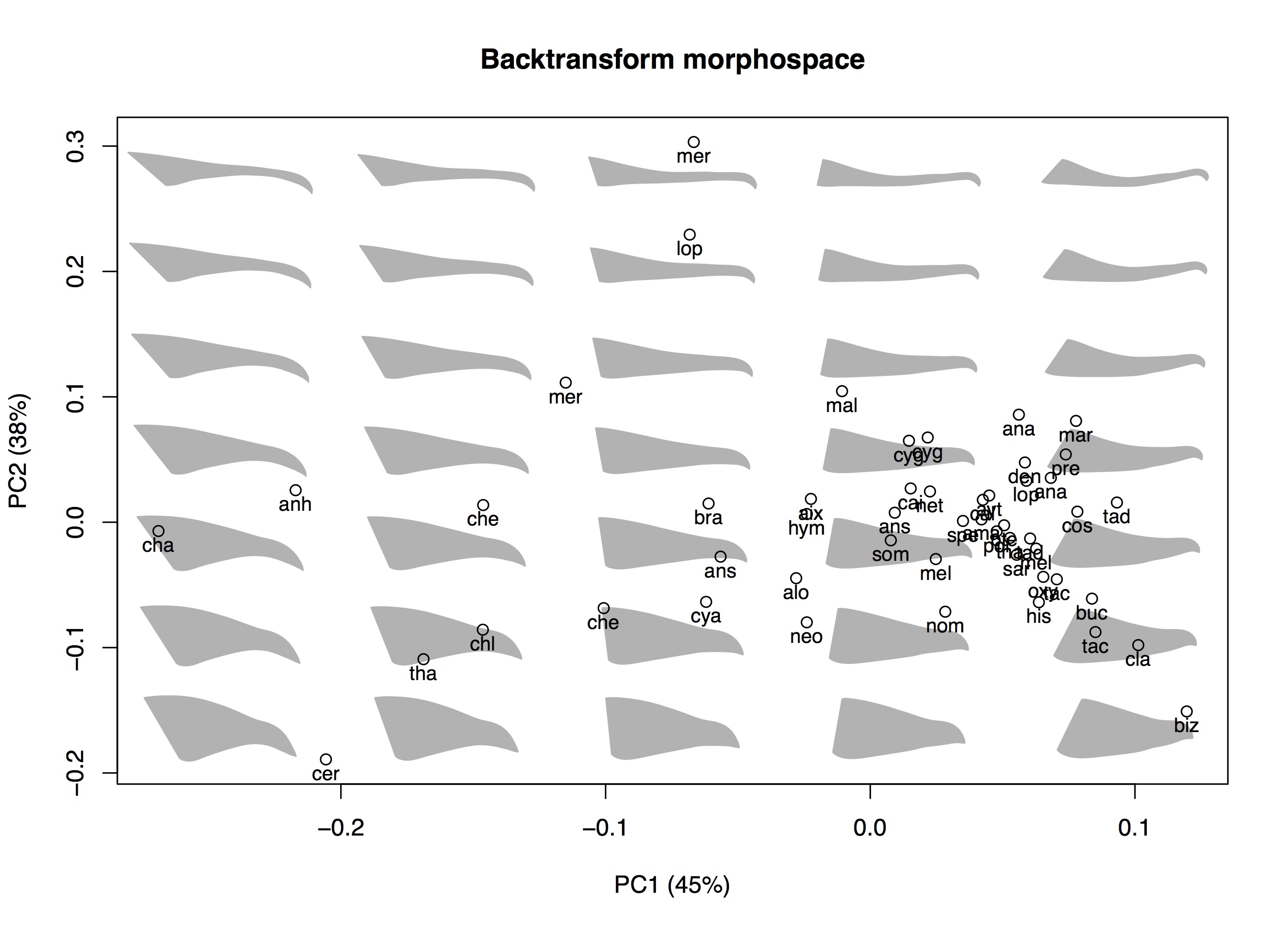
Creating a backtransform morphospace using 2D shape data
Creating a backtransform morphospace using 2D shape data only requires changes to the custom function that draws each backtransform shape (the fcn input to btShapes). You can easily convert the example dataset from this tutorial into a 2D dataset by taking only the first two dimensions. Since the beaks are initially aligned from front to back in the xy-plane this removes any data about the width of the beak. After converting the shape data into an array
# Convert list of shape data into array lm_array <- array(unlist(read_files), dim=c(dim(read_files[[1]]), length(read_files)), dimnames=list(rownames(read_files[[1]]), NULL, gsub('[.]txt$', '', list.files('Beak shape by species'))))
remove the last dimension
# Take only the first two dimensions lm_array <- lm_array[, 1:2, ]
Then you can run all of the subsequent code as before (you'll need to reduce the size parameter in btShapes from 0.5 to 0.35). Note that the m input parameter to btShapes should now be 2 versus 3. Using dim(lm_array)[2] will automatically account for this by reading the number of coordinate dimensions in lm_array.
The plot above shows the result of using 2D shape data. The backtransform shapes looks nearly identical because we've used the same two dimensions that we plotted last time (again, ignoring beak width and any shapes in that dimension). So we haven't lost any information for the 2D plane in which we are visualizing the shapes. This wouldn't be the case if we had visualized the beaks from top down.
The percent variance explained has changed a bit for each axis. And note that the positions of the various species in the plot has flipped along the x-axis ('biz' for Biziura lobata, the musk duck, has moved from the right to the left side). This doesn't have any special significance; the orientation or order of the PC scores along each axis in PCA is arbitrary and sometimes the axes get flipped when slight changes are made to the data.
Citing this tutorial
If you are using this code for a publication, please cite the following paper:
Be sure to cite the geomorph package and the R Core Team. And if you created a pPCA backtransform morphospace then you should also cite ape, phytools, and Revell 2009. You can generate the most up-to-date citations for R packages using the 'citation' function.
# Get current citation for an R package, geomorph for example citation('geomorph')
If you find an error or have a question, please contact me!